Fyzikální expedice 2003 (24

Fyzikální expedice 2003 (24.6.2003)

Chtěli jsme si ověřit naše fyzikální poznatky v praxi, a tak jsme se vydali do terénu na fyzikální expedici. Naší základnou se stala učebna fyziky, ze které jsme v průběhu dopoledne vynášeli různé měřící přístroje a vyráželi s nimi do náchodských ulic. Zde jsme sice způsobili trochu rozruchu, ale za to jsme zjistili, že fyzika není jen o teoretických poznatcích.

Na fotografii prof. Polák s pomůckami.

Jestli máte trochu času a zájem, tak bychom Vás rádi seznámili s našimi výsledky.

Měření výšky ochozu zámecké věže teodolitem

Nejprve jsme našli místo, ze kterého je dobře vidět na zámeckou věž. (Silnice u Raisovy jídelny).Teodolitem jsme zaměřovali ochoz zámecké věže. Zjistili jsme velikost úhlu, pod kterým ochoz vidíme. Potom jsme se posunuli o 40 metrů dál od původního stanoviště a znovu jsme zaměřovali stejné místo (ochoz). Zaznamenali jsme si zjištěné údaje:

a = 10´55´

b = 11´45´

d = 40m

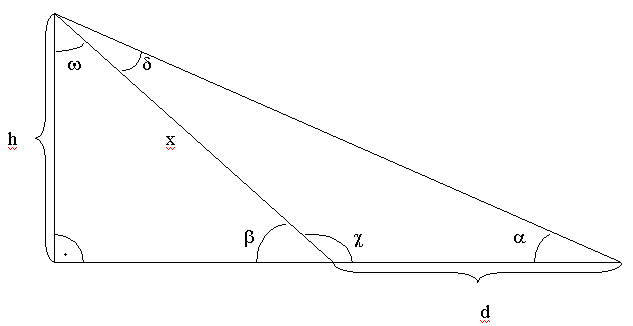
Z obrázku určíme, že c = 180´- b

d = 180´- a - c Velikost úhlu d je tedy 0´50´.

Víme, že d/sin d = x/sin a , z toho vyjádříme x:

x = d*sin a*sin b/sin d a dosadíme do vztahu h/sin b = x/sin(p/2),

z čehož plyne, že h = d*sin a*sin b/sin c

Naměřené hodnoty dosadíme do vzorce a vypočítáme výšku h: h = 106 m

Ochoz je doopravdy více než 100m vysoko nad našim stanovištěm.

Ondra Hynek (u teodolitu), zprava : Martin Smutník, Vojta Ryznar, Julie Brátová a Jana Erbenová měřící výšku ochozu zámecké věže.

Pohled na zámek od místa měření.

Měření rychlosti zvuku (Petr Vlach, Adam Rak, Ondřej Klimek)

Měřili jsme rychlost zvuku pomocí prken, kterými jsme o sebe práskali a na určité vzdálenosti stopovali, za jak dlouho uslyšíme ránu. Našli jsme vhodnou ulici v Náchodě. Zde můžete vidět její náhled.

Na jeden konec ulice se postavil někdo, kdo práskal prkny o sebe. Na druhém konci stál zbytek třídy se stopkami, poslouchali jestli uslyší ránu, a stopovali rozdíl mezi tím, co viděli a slyšeli. Změřili jsme délku ulice. Rychlost jsme spočítali pomocí vzorce : v=s/t . Jelikož bylo na konec ulice špatně vidět a díky provozu bylo i špatně slyšet, podařilo se nám změřit jen jeden čas, takže lze předpokládat celkem velkou nepřesnost. Takže délka (s) ulice byla 375m, čas(t) jsme naměřili 1,18s. Rychlost tedy vyšla 375/1,18=317,79m/s tedy asi 320m/s.

Toto měření nelze považovat za spolehlivé !

Skládání koherentních vlnění (Šimon Kvasnička, Ondřej Mika, Jakub Martinec)

Cílem pokusu bylo dokázat, že při skládání dvou koherentních vlnění dochází střídavě k zeslabení a zesílení.

Použili jsme jednoho zdroje zvuku a rozvedli jsme ho do dvou reproduktorů, aby vycházející zvuk byl stejný.

Poté každý prošel od jednoho reproduktoru k druhému ve vzdálenosti asi 3 až 4 metry a zaznamenal místo, kde intenzita zvuku byla nejmenší. (Lichý násobek l/2)

Poté jsme změřili vzdálenost od každého bodu k jednomu i k druhému reproduktoru. Jelikož jsme neměli k dispozici pásmo ( pouze metr o rozsahu 1m ) museli jsme použít přírodní měřidlo, které jsme zhotovili z prutu na který jsme udělali vždy po půl metru zářez. Spočítali jsme rozdíl vzdáleností každého bodu od obou zdrojů a rozdíl mezi dvěma sousedními rozdíly vždy tvořil vlnovou délku.

Takto vypadá tabulka hodnot:

	d₁(m)	d₂(m)	Dd (m)	DDd (m)
1	6,50	9,00	2,50	0,45
2	6,52	8,57	2,05	0,28
3	6,61	8,38	1,77	0,30
4	6,68	8,15	1,47	0,40
5	6,83	7,90	1,07	0,39
6	6,94	7,62	0,68	0,32
7	7,14	7,50	0,36	0,34
8	7,26	7,24	0,02	0,35

Legenda:

d₁– vzdálenost od prvního reproduktoru

d₂– vzdálenost od druhého reproduktoru

Dd – rozdíl vzdáleností minima od obou reproduktorů ( lichý násobek l/2)

DDd rozdíl mezi dvěma sousedními vzdálenostmi Dd ( vlnová délka l )

frekvence zvuku : f = 1000Hz

Průměrná vlnová délka činí 0.35m

Nyní můžeme spočítat rychlost zvuku v = l . f = 350 m .s^-1

Pozorování Slunce

24. června 2003 8:00 – 9:00 l. č.

1) Aktuální stav slunečního povrchu

Pomocí dalekohledu promítáme na papír sluneční kotouč. Vytváříme tak skutečný převrácený obraz Slunce. Z obrazu je patrné, jak přes zorné pole přecházejí mraky a také jsou velice dobře pozorovatelné sluneční skvrny v podobě černých teček ohraničených šedou oblastí (obraz Slunce je bledě žlutý). Toto barevné odlišení je způsobeno obrovským rozdílem ve vyzařování energie skvrnami a samotným Sluncem. Je to dáno rozdílem teplot: sluneční povrch má teplotu 6000°C, kdežto skvrny asi 5500-5700°C. V černém středu skvrny je tedy teplota asi o 500°C menší než na povrchu, šedá oblast je přechodem mezi těmito dvěma teplotami.

Z www.astronomie.cz Převrácený obraz ze školního dalekohledu

2) Jak rychle jde Slunce po obloze

Podle obrazu jsme určili, že Slunce přejde svůj průměr za 2min 17s. Měřili jsme od chvíle, kdy Slunce zcela zaplnilo zorný úhel, až do chvíle, kdy z něj zcela zmizelo. Víme, že průměr Slunce je 1,5x10⁶ km a vzdálenost Země-Slunce je 150 mil km.

Naše skupina – Lucka Kytarová, Šárka Kaplanová, Aneta Ježová, Alena Drašarová a Gábina Grulichová (zleva) pozorující převrácený obraz Slunce

3) Fresnelova čočka

Tato čočka je vypouklá a je tvořena množstvím soustředných kružnic. Použili jsme čočku přibližně 40x50 cm, která silně koncentruje paprsky a proto je silným tepelným zdrojem. Během několika sekund zapálí papír nebo propálí karton.

4) Ohřev vody koncentrovanými slunečními paprsky

a) pomocí skupiny zrcátek

Na zem jsme položili plechovku s vodou a teploměrem o počáteční teplotě 21°C. Dvacet lidí se zrcátky se postavilo do půlkruhu čelem ke Slunci a mířilo “prasátky” na plechovku. Tím jsme vytvořili tzv. Fresnelovu parabolu. Po 7, 5 min. se teplota vody zvýšila o 5 °C, ale bylo to způsobeno spíše přímým slunečním zářením, než našimi zrcátky. Plochá zrcátka jsou tedy velice málo výkonnými nástroji k ohřevu předmětů a tekutin.

b) pomocí Fresnelovy čočky

Na zemi stojí stále plechovka s teploměrem a vodou o teplotě 26 °C, namíříme na ní Fresnelovu čočku. V místě dopadu paprsku začala plechovka po několika sekundách doutnat. Voda se během dvou minut ohřála na 40 °C.

Papír se zapálí mnohem dřív, protože má tepelnou kapacitu mnohem menší než plech.

Zahřívání vody v plechovce pomocí zrcátek

Zahřívání vody v plechovce pomocí Fresnelovy čočky

Meteorologické pozorování

Provedli jsme měření tlaku a teploty vzduchu pomocí 2 barometrů a suchého a mokrého teploměru. Hodnoty jsme zapsali do níže uvedené tabulky:

Místo	Teplota vlhkého teploměru (°C)	Teplota suchého teploměru (°C)	Vlhkost vzduchu (%)	Tlak na tlakoměru 1 (kPa)	Tlak na tlakoměru 2 (kPa)	Průměrná hodnota tlaků (kPa)
park u školy	17,1	23,2	52	99,98	99,66	99,82
náměstí-pranýř	17,0	23,0	52	100,1	99,72	99,91
socha u zámeckých schodů	16,8	21,5	57	99,82	99,47	99,65
zámek-u kašny	16,5	21,1	60	99,09	98,71	98,90
ochoz věže	16,0	19,8	64	98,98	98,18	98,58

Pozn. Vlhkost vzduchu jsme zjistili z psychrometrických tabulek.

PSYCHROMETR - přístroj k přibližnému určení relativní vlhkosti vzduchu

Psychrometr se skládá ze dvou teploměrů, tzv. "suchého"a tzv "mokrého"( viz obrázek níže). "Mokrý" teploměr si vyrobímejednoduše tak, že baňku se rtutí (lihem,...) obalíme vlhkou gázou. Pro měření necháme takto připravený teploměr cca 15 - 20 minut a poté odečteme teploty z obou teploměrů. Vypočítáme rozdíly teplot na obou teploměrech a z následující tabulky určíme přibližnou hodnotu relativní vlhkosti vzduchu.

Teplota vzduchu	Rozdíl teplot na obou teploměrech
°C	1	2	2,5	3	3,5	4	4,5	5	5,5	6	6,5	7	7,5	8
0	80	60	51	41	32	22	13	4
2	82	64	55	47	38	30	21	13	5
4	84	67	59	51	44	36	29	21	14
6	85	70	63	56	48	41	35	26	21	14	8
8	86	72	66	59	53	46	40	34	27	21	15	6
10	87	74	68	62	56	50	44	39	33	27	22	16	11	6
12	88	76	70	65	59	54	48	43	38	33	28	23	18	13
14	89	78	72	67	62	57	52	47	42	37	32	28	23	19
16	89	79	74	69	64	60	55	50	46	41	37	33	28	24
18	90	80	76	71	66	62	58	53	49	45	41	37	33	29
20	91	81	77	73	68	64	60	56	52	48	44	40	37	33
22	91	82	78	74	70	66	62	58	54	51	47	43	40	39
24	91	83	79	75	71	68	64	60	57	53	50	46	43	40
26	92	84	80	76	73	69	66	61	59	55	52	49	46	43
28	92	84	81	77	74	71	67	64	60	57	54	51	48	45
30	93	85	82	78	75	72	68	65	62	59	56	53	50	47
32			83	79	76	73	70	67	64	61	58	5	52	49
34							71	68	65	62	59	57	54	51

Z těchto hodnot vypočítáme rozdíl nadmořských výšek zámecké věže a náměstí:

vysvětlivky:

Δh - rozdíl nadmořských výšek na náměstí a na věži

Δp - rozdíl tlaku na náměstí a na věži Δp = 1,24 kPa

t - průměrná teplota vzduchu t = 21,5 °C = 294,7 K

p - průměrný tlak vzduchu p = 99,20 kPa

g – tíhové zrychlení : g = 9,81m.s^-2

M_m - molární hmotnost vzduchu : M_m = 29 g/mol

Δh = 108 m

Skupina meteorologů na ochozu zámecké věže: (zleva) Michaela Tylšová, Michal Preclík, Tomáš Jirman, Vojtěch Zelený

Závěr :Výška věže vyšla podle našich výpočtů asi 108 metrů. Zjištěná výška velmi odpovídá výšce určené trigonometrickou metodou.